If the ratio of the length of AB to the length of EB is 5:1, and the area of triangle BED = 5 a 2 + 10, what is area of triangle ABC?

In the diagram above,

is

congruent to

, and

is

congruent to

.

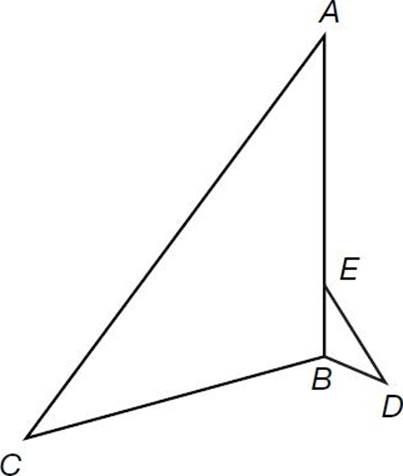
If the ratio of the length of AB to the length of EB is 5:1, and the area of triangle BED = 5 a 2 + 10, what is area of triangle ABC?
A . 5a 2 + 10
B . 25a 2 + 50
C . 25a 2 + 100
D . 125a 2 + 250
E . Cannot be determined.

Answer: D

Explanation:

Triangles ABC and BED have two pairs of congruent angles. Therefore, the third pair of angles must be congruent, which makes these triangles similar. If the area of the smaller triangle, BED, is equal to bh/2, then the area of the larger triangle, ABC, is equal to

or

. The area of triangle ABC is 25 times larger than the area of triangle BED. Multiply the area of triangle BED by 25: 25 × (5 a 2 + 10) = 125 a 2 + 250.